本記事は前回に続き、令和７年度大学入学共通テスト 試作問題『情報Ⅰ』を社会人向けに解説します。今回は設問２－Aを取り上げています。
この設問では世間的には「QRコード」と呼ばれている二次元コードについて問われています。一見すると、このコードについての知識がないと分からないように思えるかもしれませんが、実はそうではありません。
設問２－Aは情報についての詳しい知識は必要なく、読解力と論理的思考によってのみ解答することができる問題です。
文部科学省が出している「高等学校学習指導要領(平成30年告示)」 によれば、情報の科目で身に着ける力に「思考力，判断力，表現力」があります。そして、それにより「目的や状況に応じて，情報と情報技術を適切かつ効果的に活用して問題を発見・解決する方法について考え」られるようになることを目標に設定しています。
情報を正しく理解し、活用、判断できる能力は、現代の情報社会において誰しも求められるものです。設問２ーAではまさにこの能力が問われています。基礎知識も不要で、情報社会に欠かせない思考力や判断力がテーマになっているので、設問１と同様、必ず正解したい内容です。
設問２ーA：読解力と論理的思考力を問う問題
問題文
次の太郎さんと先生の会話文を読み，問い（問１～４）に答えよ。
太郎：二次元コードって様々なところで使われていて，便利ですね。
先生：二次元コードといってもいろいろ種類があるけれど，日ごろよく目にするものは日本の企業が考えたんだよ。
太郎：すごい発明ですね。企業だから特許を取ったのでしょうか。
先生：もちろん。 （ア）世の中で広く使われるようになったんだよ。
太郎：どのくらいの情報を入れられるのでしょうか。
先生：大きさにもよるけど，図１ぐらいの大きさであれば，数字なら187文字，英小文字なら78文字，記号や漢字なら48文字を入れられるよ。二次元コードの形状にはどんな特徴があるかな？
太郎：黒白の小さな正方形で構成されていて，３か所の隅に二重の少し大きな正方形がありますね。
先生：黒白の小さな正方形はセルと言って，1と0に符号化されるんだよ。図１の二次元コードは縦×横が33×33のセルで構成されているけど，文字種や文字数などによってセルの縦と横の数が変わり，それにつれて二次元コードの大きさも変わるね。Ａ３か所の隅にある二重の少し大きな正方形は，読み取り機にこの二次元コードがあることを教えている位置検出の目印なんだ。
太郎：この二次元コードって一部を隠しても正しく読み取れるんですよね。
先生：Ｂ誤り訂正機能だね。工場などでの製品管理でも使えるように，汚れや破損などで一部が読み取れなくても復元できるんだよ。読み取れない面積の割合によって復元できるレベルは４段階あるんだ。
太郎：すごい技術ですね。
先生：そうだね。自分でも二次元コードを作成できるから，いろいろ試してみたらどうかな。
図１ 二次元コードの例（令和７年度大学入学共通テスト 試作問題『情報Ⅰ』９ページ）問１
空欄（ア）に当てはまる文として最も適当なものを，次の０～３のうちから一つ選べ。
０：そこで，使用料を高くすることでこの二次元コードの価値が上がったから
１：しかし，その後特許権を放棄して誰でも特許が取れるようにしたから
２：そして，特許権を行使して管理を厳密にしたから
３：でも，特許権を保有していても権利を行使しないとしていたから
こたえと解説
こたえ：３
知っていればすぐに分かる問題ではあるものの、知らなくても「世の中で広く使われるようになった」の記述と矛盾しない選択肢を消去法で選ぶことができます。この意味では、きちんと読んで情報を整理する力が問われているといえるでしょう。
０：使用料を高くすると、使う人は減ると考えられます。
１：特許権を放棄すると、他の人に特許権を取られることが予測できます。するとその特許権を良いことにお金儲けに使われる可能性なども考えられ、「広く使われるようになった」とつながる記述であるとは言えません。
２：管理を厳密にすると、規制が増えるなどして使いづらくなり、利用者は増えにくいと考えられます。
３：正しい。権利が行使されないため、誰でも自由に使うことができます。
問２
下線部Ａの目印は，図２のように，例えば(a)～(c)のどの角度で読み取っても，黒白黒白黒の比が1:1:3:1:1となることで，二次元コードの目印として認識できるようになっている。これは，図３のように円形の目印でも同じと考えられるが，正方形の方が都合がよい。その理由として最も適当なものを，後の０～３のうちから一つ選べ。
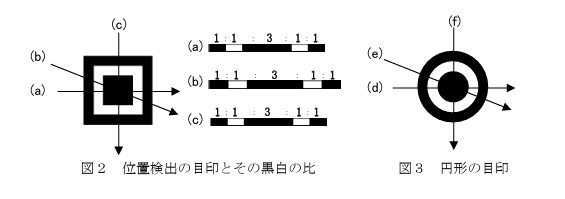
（令和７年度大学入学共通テスト 試作問題『情報Ⅰ』１０ページ）
０：円形では，(d)～(f)の角度によって黒白の比が異なってしまい，正しく読み取れなくなる可能性があるから。
１：円形だと上下左右がないので，二次元コードの向きが分からなくなるから。
２：プリンタやディスプレイの解像度によっては，正方形の目印に比べて正しく読み取れる小さな円形の目印を作ることが難しくなるから。
３：円形では目印が斜めに傾いていても，それを認識することができないため正しく読み取ることができないから。
こたえと解説
こたえ：２
二次元コードで、比率などが出てくる問題なので「難しそう」と思うかもしれませんが、読んでみると実は簡単な問題です。知識は必要なく、提示された情報をもとに選択肢を精査すれば答えが分かります。
０：実際に見てみると分かりますが、d、e、fのどの角度からでも「1:1:3:1:1」の比は変わりません。
１：目印のない角がどこにあるかによって向きを特定できます。
２：正しい。ディスプレイは四角の集まりになっているため、円を作るには四角の濃淡などの表現が必要で、最低限の解像度も必要になります。逆に、四角で四角を表すのに濃淡による表現は必要ないため、多少解像度が悪くても円よりは作成が容易です。
３：斜めに傾いても円の形は変わりません。
問３
太郎さんは，先生から二次元コードを作成することができる図４のようなWeb アプリケーションを教えてもらった。この二次元コード画像作成ツールは，二次元コード化する文字列とセルのサイズ（大きさ），誤り訂正のレベル（復元能力），画像ファイル形式を指定すると二次元コードの画像が作成できるものであった。
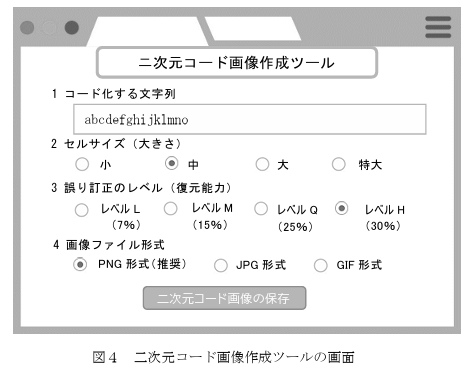（令和７年度大学入学共通テスト 試作問題『情報Ⅰ』１１ページ）
下線部Ｂについて，興味を持った太郎さんは，この作成ツールを使い，二次元コード化する文字列の長さと誤り訂正のレベルによってどのようにセルの縦と横の数が変化するか調べることにした。そこで，試しに英小文字（a～z）で構成する文字列の文字数をいろいろ変えて二次元コードを作成したところ，表１のようになった。表中のn×nはそれぞれセルの縦と横の数を表している。 なお，この作成ツールではセルの縦と横の数は自動的に最適な数に調整される。また，復元能力の値(％)が大きいほど誤りを訂正する能力が高いことを表
し，例えば，復元能力30％は，二次元コードの面積の最大30％が読み取れなくてもデータを復元できることを意味する。
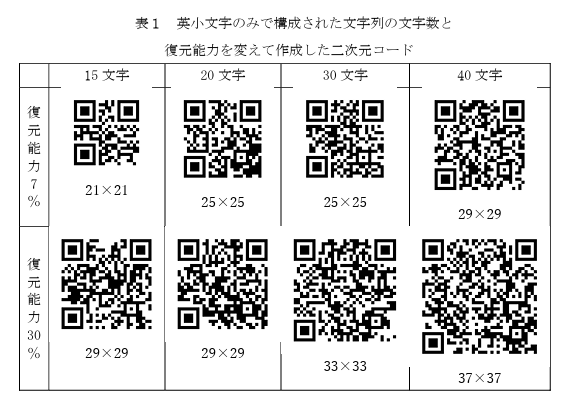（令和７年度大学入学共通テスト 試作問題『情報Ⅰ』１２ページ）
この表１の結果から考えられることとして適当なものを，次の０～５のうちから二つ選べ。ただし，解答の順序は問わない。
０：同じ復元能力であれば，文字数に比例してセルの数が多くなり，同じセルの大きさであれば二次元コードも大きくなる。
１：復元能力ごとに，文字数の一定の範囲でセルの縦と横の数が決まり，文字数が多くなるほど段階的にセルの縦と横の数は多くなる。
２：文字数とセルの数には関係が見られない。
３：ある文字列を復元能力30％で作成した二次元コードは，同じ文字列を復元能力7％で作成したものに比べ約4倍のセルの数がある。
４：復元能力30％にするためには，復元能力7％と比べより多くの情報が必要となる。
５：同じ文字数であれば復元能力を変えてもセルの数は変わらない。
こたえと解説
こたえ：１，４
これも、問題文をもとに表と選択肢を照らし合わせれば解ける問題です。
０：7%の場合の20文字と30文字の二次元コードを見ると分かるように、文字数とセルの数は比例していません。
１：正しい。7%の場合は15文字と20文字の間、30文字と40文字の間、30%の場合は20文字と30文字の間、30文字と40文字の間でセルの数が変わっています。1文字増えるごとにセルの数が変わるのではなく、一定の範囲で段階的にセル数が多くなっていることが分かります。
２：上記の選択肢１の解説のように、文字数の範囲に応じてセルの数も増えていくため、関係があります。
３：同じ文字数で7%と30%の場合のセルの数を実際に計算してみましょう。15文字の場合、7%は21×21=441、30%は29×29=841です。2倍にも満たないことが分かります。
４：正しい。同じ文字数でも、復元能力を上げるとセルの数が増えています。
５：15文字の場合を見てみると、7%は「21×21」、30%は「29×29」です。セルの数は明らかに異なります。
問４
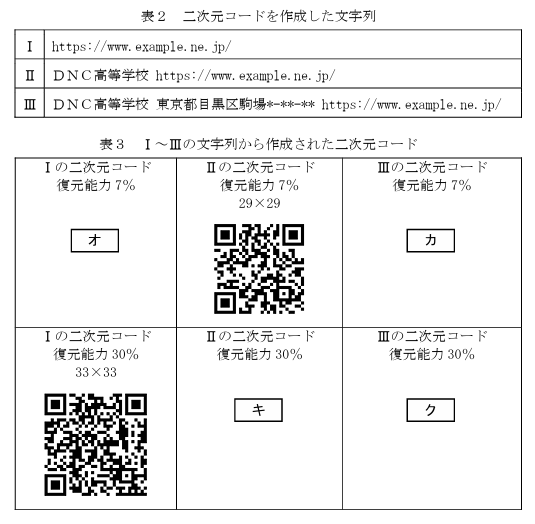
次に，太郎さんは，図４のWebアプリケーションを使って試しに表２のⅠ～Ⅲの三つの文字列について二次元コードを作成してみた。復元能力は７％と30％の両方を作成し，セルサイズもいろいろ変えてみたところ，表３に示す二次元コードが作成された。その結果，復元能力７％と30％のそれぞれにおいて作成された二次元コードのセルの数は，Ⅰ～Ⅲの文字列で異なっていた。また，Ⅰ～Ⅲの文字列はアルファベットや記号，漢字などが含まれているので，表１の英小文字のみで構成された文字列の文字数とセルの縦と横の数の関係には必ずしもなっていないことが分かった。表３の空欄 （オ） ～（ク） に当てはまる適当な二次元コードを，後の解答群のうちから一つずつ選べ。
（令和７年度大学入学共通テスト 試作問題『情報Ⅰ』１３ページ）
（令和７年度大学入学共通テスト 試作問題『情報Ⅰ』１４ページ）
こたえと解説
こたえ：（オ）２（カ）０（キ）３（ク）１
これまでの問題の情報をもとに解く問題です。
まずは情報を整理しましょう。表２はⅠ、Ⅱ、Ⅲの順に文字数が増えています。ということは、同じ復元能力の場合にはこの順にセル数が増える（または同じ）と考えられます。
このことから、Ⅰの7%が最もセル数が少なく、Ⅲの30%が最もセル数が多くなることが分かるので、（オ）には２、（ク）には１が入ることが分かります。
そして（カ）には、左にあるⅡの7%（29×29）より大きく、下にあるⅢの30%（49×49）より小さいものを選べば良いと分かるので、０が答えです。
（キ）には残った３が入り、実際にあてはめてみてもⅠの30%（33×33）より大きく、Ⅲの30%（49×49）より小さいため合っていることが分かります。
※この問題の場合、どの範囲で段階的に増えるかは分からないので、範囲のことは想定せずにセル数のみで考えています。
まとめ
実際に内容と解説を見てみると、しっかり読めば分かるものばかりだと理解いただけたのではないでしょうか。同時に、整理しなければならない情報の難易度も体感いただけたのではないかと思います。
現代社会においても、身の回りにあふれている情報は単純なものばかりではなく、自分で整理したり補ったりしなければなりません。いま求められているリテラシーのレベルは、想定しているより高いものかもしれません。
次回の２－Bも情報を扱う力が問われる問題です。同じように、社会人ならば必ず正解したい問題なので、次回もぜひご覧ください。
